Part One: History of the Quartic In 1540, Cardan was given the following problem:
Divide 10 into 3 parts: The parts are in continued proportion and the product of the first 2 is 6
This problem lead to a quartic which Cardan was not able to solve. He gave it to Ferrari. Ferrari was the first to develop an algebraic technique for solving the general quartic. He applied his technique (which was published by Cardano ) to the equation
x4 + 6x2 - 60x + 36 = 0 Part Two: Solving The Cubic (Theory) A general quartic equation (also called a biquadratic equation) is a fourth-order polynomial equation of the form
|        | Using the same substitution as in the cubic case one can transform this quartic to the following reduced (or standard) form
where
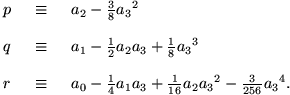 The quartic can be solved by writing it in a general form that would allow it to be algebraically factorable and then finding the condition to put it in this form. The equation that must be solved to make it factorable is called the resolvent cubic.
|




