Unlike quadratic, cubic, and quartic polynomials, the general quintic cannot be solved algebraically in terms of a finite number of additions, subtractions, multiplications, divisions, and root extractions, as rigorously demonstrated by Abel (see Part Two: Abel's impossibility theorem) and Galois.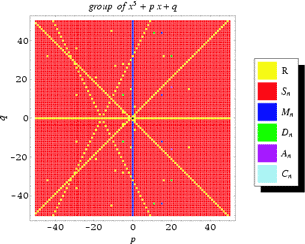

However, certain classes of quintic equations can be solved in this manner. Irreducible quintic equations can be associated with a Galois group, which may be a symmetric group S_n, metacyclic group M_n, dihedral group D_n, alternating group A_n, or cyclic group C_n, as illustrated above.

Euler reduced the general quintic to

A quintic also can be algebraically reduced to principal quintic form

By solving a quartic, a quintic can be algebraically reduced to the Bring quintic form