as was first done by Jerrard. Runge (1885) and Cadenhad and Young found a parameterization of solvable quintics in the form

by showing that all irreducible solvable quintics with coefficients of x⁴, x³, and x² missing have the following form

where and are rational.

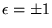
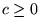
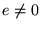
Spearman and Williams (1994) showed that an irreducible quintic of the form x⁵ + ax + b = 0 having rational coefficients is solvable by radicals iff there exist rational numbers , , and such that

The roots are then

where