and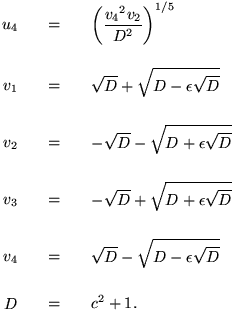

In the case of a solvable quintic, the roots can be found using the formulas of Malfatti (1771), who was the first to "solve" the quintic using a resolvent of sixth degree (Pierpont 1895).

The general quintic can be solved in terms of Jacobi theta functions, as was first done by Hermite in 1858. Kronecker subsequently obtained the same solution more simply, and Brioshi also derived the equation.

"In general, polynomial equations higher than fourth degree are incapable of algebraic solution in terms of a finite number of additions, subtractions, multiplications, divisions, and root extractions." Published in 1824 at his own expense, the pamphlet was dismissed by Gauss who failed to recognize that the famous problem had indeed been settled.